GPS is an earth positioning system capable of detecting the exact location of a point in space, this tracking system was designed by the U.S. Department of Defense (DOD). GPS works through 32 orbiting satellites, plus some backup ones. These orbits are circular on 6 parallel orbital planes inclined 55° to the equatorial plane and are about 20 km away from the earth. The satellites make two rotations of the planet per day.
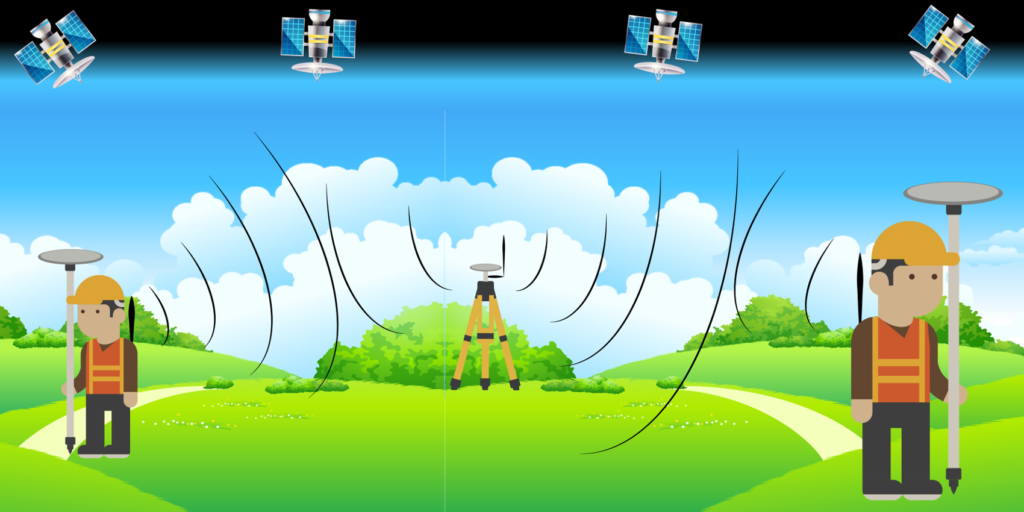
The GPS system is designed so that at least 4 satellites, which are necessary and sufficient for the use of the system, are observable from every point on earth under all weather conditions.
GPS has been operational since 1994 but, even today satellites are still being launched into orbit to keep the number of operational satellites always high.
Most of the satellites were placed in orbit by launching (disposable) rockets. In addition to the satellites, there are also 4 ground control stations critical to the system, which otherwise would not function, because such a system requires constant verification of the status of the satellites, and correction of their atomic clocks and orbital position. Maintenance of the system therefore is essential, in fact any suspension of it would cause the system to decay within a few days and be completely useless after about 2 weeks.
Each GPS receiver performs these operations:
- Locates 4 or more available satellites;
- Calculate the distance to each of the satellites (assuming constant radio wave propagation speed);
- It uses the received data to compute its own position by the process of trilateration: since the positions of the satellites in space and the distance of the receiver from each satellite are known, an intersection of 4 spheres is obtained, which degenerates to a point at less than acceptable accuracy.
Here is how the measurement process takes place: at a predetermined time (let’s assume 2:00 p.m.) the satellite generates a code (called pseudo random code) and sends it back to earth. Also at 2:00 p.m., the GPS receiver also generates the exact same code so that when the signal from the satellite arrives on the ground and is read by the receiver, that receiver knows the time the signal started and thus is able to measure how long it took the signal to arrive.
The distance between the satellite and the GPS receiver is obtained by the latter by multiplying that time by the speed of light (299,792 km/s), which is equal to the propagation speed of the radio waves used to send the signal. Once the distance is obtained, the receiver knows that it is on a point on the sphere whose radius is that distance and whose center is the position of the satellite. Repeating this operation for at least four satellites results in a sphere for each satellite. The intersection of these spheres degenerates to a point at less than acceptable accuracy.
Precision GPS receivers have a precise internal chronometer: an error on the chronometer of 0.00000001 seconds would correspond to an error of as much as 3 centimeters on the sphere measurement.
The satellites’ internal clocks must be even more accurate since a dyssynchrony would affect all measurements around the world. Therefore generally the satellites house as many as four very expensive atomic clocks costing about 160,000 euros, which exploit the oscillations of cesium and rubidium atoms and guarantee an absolute standard of accuracy. In fact, the possibility of error is one second every 30,000 years.
One notable curiosity is this: according to the theory of relativity, because of relative velocity, satellites travel into the future and therefore their clocks must undergo a correction to be synchronized with ground clocks! The design engineers, who did not believe in time travel, put two computational mechanisms on the first satellites: one that took into account the fact that satellites travel into the future and one that ignored that. The result was that, without the relativistic correction, the GPS system presented incorrect calculations. Thus Albert Einstein’s theory of relativity was confirmed by, among other things, the current operation of GPS satellites.
But what would happen if the signal arrived at the receiver by bouncing off other surfaces first? The imaginary line joining the satellite and the receiver would no longer be straight, it would have crossing points and therefore the calculation of the distance between satellite and receiver would be distorted, this is the phenomenon of Multipath, we discussed about it.


